



Next: M-filer
Up: Basal brug af MATLAB
Previous: Databehandling
Contents
Index
Subsections
Grafik
En del af MATLABs funktioner tjener til at konstruere grafiske
præsentationer. I dette afsnit vises kun nogle enkle muligheder for 2-D
og 3-D grafik. Ved mere avanceret brug anbefales det, at konsultere MATLABs
egne manualer.
2-Dimensional grafik
Den mest elementære funktion til at tegne grafer med er plot funktionen.
Denne tager en vektor som inputparameter og producerer en stykvis lineære graf af
elementerne i vektoren versus indeks af elementerne i vektoren. F.eks.
en vektor hvis elementer svarer til et datasæt. plot kan også tage to
vektorer x og y til input og funktionen vil producere en graf af vektor y
versus vektor x.
Først kunstrueres en vektor x og man vælger f.eks. at anvende randn-funktionen. Der skrives x = randn(15,1) på kommandolinien.
Herefter plottes vektoren x ved at taste:
plot(x)
Resultatet vil nu vises i figurvinduet, se på figur
2.2. Som standard, forbinder plot de enkelte
punkter med en ret linie.

Figure 2.2:
Dette er plottet af en vektor, hvis element er genereret
udfra randn-funktionen
|
|
En matematisk funktion kan plottes ved at anvende plot funktionen med
to vektorer som input![[*]](/usr/share/latex2html/icons/footnote.gif) . Vektoren t skal fungere som første akse. Denne angiver
således et interval og en intervalinddelling mellem de punkter
hvorudfra grafen konstrueres. F.eks. skrives: t = 0.025: 0.025 : 10 på
kommandolinien. Intervallet er nu [0.025,10] og skridtlængden er
0.025. Herefter konstrueres vektoren y, der indeholder
funktionensværdierne. Funktionen er her den naturlig logaritmefunktion og for
vektoren y skrives y = log(t). Det er muligt at angive om
grafen skal bestå af adskilte punkter,
eller være en sammenhængende kurve. Om det skal være krydser eller stjerne som
punkter eller om det skal være en fuld optrukken eller stiplet linie.
Samlet kan dette opskrives som:
. Vektoren t skal fungere som første akse. Denne angiver
således et interval og en intervalinddelling mellem de punkter
hvorudfra grafen konstrueres. F.eks. skrives: t = 0.025: 0.025 : 10 på
kommandolinien. Intervallet er nu [0.025,10] og skridtlængden er
0.025. Herefter konstrueres vektoren y, der indeholder
funktionensværdierne. Funktionen er her den naturlig logaritmefunktion og for
vektoren y skrives y = log(t). Det er muligt at angive om
grafen skal bestå af adskilte punkter,
eller være en sammenhængende kurve. Om det skal være krydser eller stjerne som
punkter eller om det skal være en fuld optrukken eller stiplet linie.
Samlet kan dette opskrives som:
t = 0.025: 0.025 : 2
y = log(t)
plot(t,y,'--')
Her er angivet at grafen skal være en stiplet linie ved at taste
to bindestreger mellem to enkel citationstegn. Citationstegnene er vigtige,
fordi de fortæller MATLAB, at her kommer en angivelse af grafens
udseende. Bemærk, at rækkefølgen af t og y viser, at t ønskes ud af 1-aksen
og y ud af 2-aksen. Resultatet vises i figurvinduet og ses
på figur 2.3.
Figure 2.3:
Dette er plottet af den naturlige logaritme, hvor
grafen er tegnet med en stiplet linie.
|
|
Fordi den matematiske funktion her er en logaritmisk funktion, kunne det
have interesse med akser, der er logaritmisk inddelt. Dette kan let
gøres ved at anvende hjælpefunktionen semilogx istedet for plot. Der tastes
semilogx(t,y,'--')
Og figuren i figurvinduet ændres til de nye akser. Resultatet kan ses på
figur 2.4
Figure:
Dette er plottet af den naturlig logaritme funktion,
hvor første aksen er inddelt logaritmisk. Kun de positive data plottes
|
|

Udover at kunne angive hvilke typer af linier og punkter, der ønskes
anvendt i grafen kan eventuelle farver også specificeres. Hvis f.eks.
der ønskes en rød graf skrives 'r-' istedet for '-'. Er der ingen
angivelse af farve og form er MATLABs default indstilling en fuld optrukken blå
linie. I tabellen 2.1 ses en oversigt over de angivelser, der
kan anvendes.
Table 2.1:
Oversigt over de symboler, der kan anvendes til at angive
grafens stil.
| symbol |
farve/linie |
symbol |
punkt stil |
| y |
gul (yellow) |
. |
prik |
| m |
magentarød |
o |
cirkel |
| c |
cyan |
x |
kryds |
| r |
rød |
+ |
plus |
| g |
grøn |
* |
stjerne |
| b |
blå |
s |
firkant |
| w |
hvid (white) |
d |
diamant |
| k |
sort (black) |
v |
trekant (op) |
| - |
fuldt optrukken |
< |
trekant (venstre) |
| : |
prikket |
> |
trekant (højre) |
| -. |
stiplet/prikket |
p |
pentagram |
| - |
stiplet |
h |
hexagram |
Det er muligt at plotte to eller flere grafer i samme figur. Dette kan gøres på
to
forskellige måder. Her vil dette blive vist ved at udvide forrige eksempel.
I forrige eksempel konstrueres vektorerne t = 0.025: 0.025 :2 og y
= log(t). Her generes en ny vektor x ved at skrive x = t .* log(t).
Graferne for y og x begge versus t ønskes nu i samme figur. Grafen for y skal
være en fuld optrukken rød linie, mens x ønskes markeret som en blå
stiplet linie. Der ønskes igen anvendt lineære akser. På kommandolinien
tastes nu:
plot(t,y,'r-',t,x,'b--')
Bemærk, at det er vigtigt at angive t igen som 1-akse ved grafen for x.
Den anden løsning er at benytte de specielle kommandoer hold on og
hold off. hold on kommandoen sørger for, at MATLAB ikke fjerner
tidligere grafer, når en ny graf skal tegnes. Det kan dog være nødvendigt at
omskalere akserne, men den oprindelige graf vil da blive overført til de
nye akser. Når hold on effekten ikke ønskes mere skrives hold
off. Graferne for y og x kan således blive tegnet ganske tilsvarende ved
at skrive:
hold on
plot(t,y,'r-')
plot(t,x,'b--')
hold off
På figur 2.5 ses resultatet. I dette sort-hvide tryk vil
farverne af graferne naturligvis ikke kunne gengives.
Figure 2.5:
Her er plottet de to funktioner log(t) (fuld optrukken) og t*log(t)
(stiplet).
|
|

Når grafen for det ønskede er plottet i figurevinduet, kan der tilføjes
læsevejledende tekster til vinduet. Der er flere hjælpefunktioner her til.
- title('tekst') Denne funktion sætter den
titel,
der er angivet mellem de to citationstegn, på figurvinduet.
- xlabel('tekst') Her sættes en tekst på første aksen
af figuren.
- ylabel('tekst') Med denne funktion anbringes en
tekst på anden aksen af figuren.
- text(x,y,'tekst') Her placeres teksten ind på grafen
på det punkt, der er angivet ved koordinaterne x og y.
- gtext('tekst') Nu placeres teksten ind på
grafen der, hvor man markerer med musen.
- legend('tekst1','tekst2,...) Laver
en box med tekst til de enkelte grafter. Boxen kan flyttes
rundt med musen
3-Dimensional grafik
Af de talrige 3-dimensionale grafik muligheder som MATLAB byder på
er det kun kurver og simple flader, der vil blive gennemgået.
Den 3-dimensionale udgave af plot hedder plot3. Denne
funktion tager tre vektorer adskilt af kommaer, som input og rækkefølgen
angiver, hvilke der er 1. 2. og 3. akse.
Som i det 2-dimensionale tilfælde angives her vektorerne f.eks. x y og z
og MATLAB konstruerer en 2-dimensionel projektion af denne 3-D figur.
Først angives her vektoren x og herefter de
funktioner som y og z skal repræsentere. Samlet kan dette skrives som:
x = 0: pi/25 : 40
y = cos(x)
z = sin(x)
plot3(z,y,x)
Ved 3-D plot kan ligeledes angives farve samt linie- og punktstil, som
for 2-D grafer. Her i eksemplet anvendes blot defaultværdien.
Tilsvarende kan der tilføjes titel og akse-tekster, samt indføres
tekster i grafen. Til den tredje akse anvendes funktionen zlabel('tekst')
og for tekster i grafen angives punktet med 3 koordinater
text(x,y,z,'tekst'). Grafen for dette eksempel kan ses på
figur 2.6.

Figure:
Denne graf viser en 2-D projektion af kurven
(
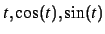 ).
).
|
|
Ved gitter-grafer plottes punkter af z koordinater over et
rektangulær gitter i xy-planen. Nabopunkter forbindes med en lige linie
og derved fremkommer effekten af en flade. Funktionerne af typen
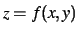 kan tegnes ved sådanne grafer. Domænet for funktionen z kan opfattes
som et gitter i xy-planen. Dette gitter reprænsenteres ved hjælp af 2
matricer X og Y. X matricen indeholder alle planens x-koordinater og
tilsvarende indeholder Y alle y-koordinaterne. Disse matricer X og Y anvendes
til at beregne værdierne for z-funktionen, samt til at konstruere grafen
for z.
kan tegnes ved sådanne grafer. Domænet for funktionen z kan opfattes
som et gitter i xy-planen. Dette gitter reprænsenteres ved hjælp af 2
matricer X og Y. X matricen indeholder alle planens x-koordinater og
tilsvarende indeholder Y alle y-koordinaterne. Disse matricer X og Y anvendes
til at beregne værdierne for z-funktionen, samt til at konstruere grafen
for z.
Den graf, der skal konstrueres er funktionen for
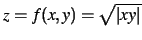 . Hjælpefunktionen meshgrid(x,y) tager to vektorer som
input og producerer de to matricer X og Y. Rækkerne i X er kopier af vektor
x og søjlerne i Y er kopier af vektoren y. Dette gøres ved at skrive:
. Hjælpefunktionen meshgrid(x,y) tager to vektorer som
input og producerer de to matricer X og Y. Rækkerne i X er kopier af vektor
x og søjlerne i Y er kopier af vektoren y. Dette gøres ved at skrive:
x = -10 : 0.5 : 10
y = x
[X,Y] = meshgrid(x,y)
Her vil domænet blive kvadratisk, idet x og y er identiske. Der defineres
nu funktionen 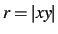 . Ved den videre behandling af z-funktionen
opfattes denne som
. Ved den videre behandling af z-funktionen
opfattes denne som
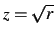 . Når z er defineret som en matrix Z anvendes
hjælpefunktionen mesh til at plotte denne matrix. Dette kan skrives
ved:
. Når z er defineret som en matrix Z anvendes
hjælpefunktionen mesh til at plotte denne matrix. Dette kan skrives
ved:
R = abs(X.*Y)
Z = sqrt(R)
mesh(X,Y,Z)
Her anvendes hjælpefunktionen abs den absolutte funktion. Grafen for
funktionen z kan ses på figur 2.7.

Figure:
Eksempel på en gitter graf.
|
|




Next: M-filer
Up: Basal brug af MATLAB
Previous: Databehandling
Contents
Index
Bo Jakobsen
2000-08-15
![]()
![\includegraphics[scale=0.5]{logt.eps}](img24.gif)
![\includegraphics[scale=0.5]{semilogt.eps}](img25.gif)
![]()
![]()
![]() kan tegnes ved sådanne grafer. Domænet for funktionen z kan opfattes
som et gitter i xy-planen. Dette gitter reprænsenteres ved hjælp af 2
matricer X og Y. X matricen indeholder alle planens x-koordinater og
tilsvarende indeholder Y alle y-koordinaterne. Disse matricer X og Y anvendes
til at beregne værdierne for z-funktionen, samt til at konstruere grafen
for z.
kan tegnes ved sådanne grafer. Domænet for funktionen z kan opfattes
som et gitter i xy-planen. Dette gitter reprænsenteres ved hjælp af 2
matricer X og Y. X matricen indeholder alle planens x-koordinater og
tilsvarende indeholder Y alle y-koordinaterne. Disse matricer X og Y anvendes
til at beregne værdierne for z-funktionen, samt til at konstruere grafen
for z.
![]()