Databehandling

I de tidligere afsnit er matricer blevet behandlet som matematiske størrelser, men der er også blevet set på matricer som tabeller, hvorpå man ønsker at behandle elementerne enkeltvis. MATLAB tilbyder muligheder for flere operationer med henblik på matricer. Det kan f.eks. være relevant at beregne gennemsnitsværdier eller summen af elementerne i en kolonne, svarende til en søjle i matricen.

Funktioner

Følgende er en oversigt over de væsentligste funktioner, der kan anvendes på matricer og på vektorer. Funktionerne er afhængige af om der opereres på en matrix eller en vektor. Efter præsentationen følger enkelte eksempler på anvendelse af nogle af funktionerne.

• max(x) Hvis x er en vektor vil resultatet af denne funktion være det største element i vektoren. Når x er en matrix vil funktionen returnere en række-vektor, hvis elementer er de største elementer fra hver af søjlerne i x.

• min(x) Hvis x er en vektor vil resultatet af denne funktion være det mindste element i vektoren. Hvis x er en matrix vil funktionen returnere en række-vektor, hvis elementer er de mindste elementer fra søjlerne i x.

• mean(x) Funktionen beregner gennemsnittet af elementerne i vektoren x. Hvis x er en matrix er resultatet en række-vektor, hvis elementer er gennemsnitsværdien for hver søjle i x.

• median(x) Her beregnes medianen for elementerne i vektoren x. Er x en matrix vil funktionen returnere en rækkevektor hvis elementer er medianen for hver søjle i x. Anvendelsen af denne funktion indbefatter en sortering af elementerne i x, derfor kan udførelsen af denne være ret omfattende for store matricer.

• std(x) Standard afvigelsen eller spredningen er af elementerne i vektor x beregnes med denne funktion. I det tilfælde at x er en matrix, vil funktionen give en rækkevektor som svar. Elementerne i denne vil være den beregnede spredning for hver af søjlerne i matricen x.

• sort(x) Sorteringsfunktionen sorterer elementerne i vektoren x i voksende orden. Er x en matrix vil hver søjle blive sorteret i voksende orden. Der returneres således en vektor eller en matrix, der er sorteret.

• sum(x) Funktionen beregner summen af elementerne i vektoren x. Når x er en matrix vil der blive returneret en vektor, hvis elementer er summen af hver søjle i x.

• prod(x) Svarende til sumfunktionen beregner denne funktion produktet af elementerne i vektoren x eller returnere en rækkevektor med produkterne af elementerne i hver søjle af matricen x.

• hist(x) Denne funktion beregner og plotter histogramer. Der konstrueres et 10 stk. bjælke-histogram af elementerne i vektoren x.

Præsentationen af funktionerne her er kun den skrabede udgave af deres anvendelse. Det kan anbefales at konsultere MATLABs egen manual (``Reference Guide''), eller benytte MATLABs doc kommando, hvis der er behov for en mere udvidet anvendelse og/eller for at se flere eksempler på anvendelser.

Eksempel

Først anskaffes en matrix x, ved at anvende magic-funktionen, der konstruerer tilfældige blandede n 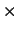$\times$ n matricer af tallene 1 til 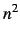$n^2$. Her er n = 4.

      x = magic(4)

Der f.eks. giver følgende resultat:

      x = 
          16     2     3     13
           5    11    10      8
           9     7     6     12
           4    14    15      1

Nu kan sorteringsfunktion anvendes på matricen x. Der skrives :

      sort(x)

Og svaret der fremkommer bliver:

      ans =
           4     2     3      1
           5     7     6      8
           9    11    10     12
          16    14    15     13

$\Box$

Eksempel

Her startes med at skaffe en vektor x bestående af 100 elementer. Disse genereres ved hjælp af talgeneratoren randn. Derfor skrives først:

      x = randn(100,1);

Hvorved en 100 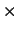$\times$ 1 matrix konstrueres. Semikolonnet, der står efter udtrykket fortæller MATLAB, at resultatet ikke ønskes udskrevet på skærmen. Dette er tit at foretrække fordi udskrivning til skærmen er tidskrævende. Den eksakte værdi af vektorens komponenter er uinteressant i denne forbindelse. Nu kan histogramfunktionen anvendes.

      hist(x)

Plottet der nu konstrueres vil ikke blive vist i kommandovinduet, men i et specielt figurvindue, der automatisk bliver åbent, hvis det ikke allerede er åbent. Man kan eventuelt bladre hen til dette nye vindue, ved hjælp af Windows-menuen. Under Windows-menuen vises titlerne på de vinduer der er åbne. Ved at vælge 1 Figure punktet vil figurvinduet komme i forgrunden af de åbne vinduer. Man kan også bladre imellem alle åbne vinduer ved hjælp af ALT TAB tasterne. Histogrammet er vist på figur 2.1.

$\Box$

Figure 2.1: Dette er histogrammet, der plottes i figurvinduet ved anvendelse af funktionen hist.

Manglende elementer

Når man arbejder med datamateriale på matrixform forekommer det, at der mangler data på enkelte pladser i matricen. Disse ``tomme'' felter kan det være hensigtsmæssigt at have med i matricen. Man kan vælge at benytte en udvalgt værdi til at markere hullerne i matricen, f.eks. 0 , -1 eller et stort tal (opfattet som 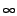$\infty$). Men dette vil medføre et misvisende resultat, hvor der skal beregnes på værdierne, f.eks. når der beregnes gennemsnittet for en søjle. I stedet kan man anvende betegnelsen NaN (Not-a-Number). Valget af NaN, løser imidlertid ikke problemerne ved beregningerne. I de fleste beregninger, hvor resultatet afhænger af dette element vil resultatet blive NaN. Af de ovenfor nævnte funktioner kan kun sort funktionen uden problemer anvendes selvom matricerne indeholder NaN elementer.

At anvende NaN til de manglende dataelementer betyder således, at de fleste hjælefunktioner er ubrugelige. Til gengæld undgås de misvisende resultater ved databehandlinger, der ikke afslører, at der er huller i datamaterialet.