Matrixoperationer

I det indledende afsnit blev det vist, hvorledes en matrix oprettes via kommandolinien. Der er flere andre metoder til at indføre matricer i Workspace på. Ved hjælp af de indbyggede hjælpefunktioner er det muligt at oprette specielle typer af matricer. Derudover kan matricer indføres via M-filer eller externe datafiler. Disse muligeheder vil blive uddybet senere i kapitel 3. Den simpleste metode er at taste matricerne ind på kommandolinien. Matricen indtastes rækkevis og:

• de enkelte elementer adskilles af blanktegn eller komma

• elementerne omklammes med firkantede parenteser, [ ]

• afslutningen af en række (alle pånær den sidste) markeres med et semikolon;

Notationer mv. specielt til vektorer gives ikke, idet vektorer opfattes som specialtilfælde af matricer.

Transponering

Den matrix, der ønskes transponeret markeres med en apostrof '.

Eksempel

Matricen A er igen defineret som A = [9 8 7;6 5 4;3 2 1]. Der ønskes en matrix B, der skal være den transponerede af matricen A. Der skrives:

     B = A'

Herved fremkommer:

     B =
         9   6   3
         8   5   2
         7   4   1

Hvis det ligeledes ønskes at transponere søjle vektoren x=[1; 3; 5; 4; 2], skrives

     p = x'

og svaret bliver

     p = 
         1  3  5  4  2

$\Box$

Addition og subtraktion

Som for skalar anvendes symbolerne + og - for henholdsvis addition og subtraktion. Det er vigtigt, at de indgående størrelser har samme dimension, for at operationen kan finde sted. Når A og x er defineret som i ovenstående eksempel vil udtrykket A + x således ikke give nogen mening og vil resultere i en fejlmeddelelse. Denne vil typisk fortælle at operationen ikke kan udføres, fordi de indgående størrelser ikke har samme dimension.

Eksempel

Der oprettes en ny matrix C, der er summen af matricerne A og B.

     C = A + B

og svaret bliver

     C =
         18   14   10
         14   10    6
         10    6    2

$\Box$

Multiplikation

Som ved skalarmultiplikation bruges stjernesymbolet * ved matrixmultiplikation. Den indre dimension af de to faktorer skal være ens for at operationen giver mening. For matricer gælder det specielt, at første faktors 2. dimension skal svare til anden faktors 1. dimension. Der er både defineret indre og ydre produkter.

Eksempel

Givet vektorene y og z, hvor y = [1 2 3] og z = [-1 0 1]. Det indre produkt beregnes ved at skrive:

     y*z'

Der resultere i svaret:

     ans =
           2

Tilsvarende kan z*y' beregnes. Forkortelsen ''ans'' står for answer og er standardsvaret, hvor resultatet ikke er specificeret til et bestemt variabelnavn. ans indgår herefter som en variabel. Derimod er

     y'*z

et ydre produkt og vil resultere i svaret:

     ans =
           -1    0    1
           -2    0    2
           -3    0    3

$\Box$

Produkter mellem matricer og vektorer, kræver ligeledes overenstemmelser i dimensionerne.

Eksempel

Her benyttes matrix A og vektor z fra tidligere eksempler.

     b = A*z'

resulterer i svaret:

     b =  
         -2
         -2
         -2

Det er vigtigt, at det er den transponerede af z, som anvendes. A*z opfylder ikke kravet til dimensionerne og vil resultere i en fejlmeddelelse.

$\Box$

Division

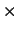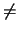Der er to symboler for division / og \. Det er udelukkende i de tilfælde, hvor A er en ikke-singulær n $\times$ n matrix (det(A) $\neq$ 0), at disse symboler korresponderer med henholdsvis højre og venstre multiplikation. Det vil sige at

• X = A\B er løsning til A*X = B

• X = B/A er løsning til X*A = B

Inden division med matricer er det således relevant at undersøge matricens determinant. Er A en matrix, skrives det(A) på kommandolinien og determinanten beregnes.

Singulære eller næsten singulære matricer er et generelt problem ved numerisk behandling af matricer. Det kan således være hensigtmæssigt at beregne en matrixs konditionstal, der er et udtryk for, hvor ''singulær'' en matrix er. MATLAB foretager selv den slags undersøgelser af matricer inden udførelsen af visse funktioner. Konditionstallet af en matrix A beregnes ved at skrive cond(A). Svaret er et meget stort tal (med en stor 10-potens), hvis matricen er singulær og meget mindre hvis den ikke er singulær. Funktionen rcond beregner den reciprokke værdi af konditionstallet. A er langt fra at være singulær hvis svaret er nær ved 1.0, mens A er næsten singulær hvis svaret er tæt ved 0.0 (nul).

Eksempel

Først et eksempel på en ikke-singulær matrix F og en søjlevektor g. Lad F = [5 0 1; -2 4 0; 3 2 1] og g = [2 ;-1 ;1]. Først udberegnes produktet

     h = F*g

hvilket resulterer i svaret:

     h =  
         11
         -8
          5

Dette kan testes ved:

     F\h

Der gives svaret:

     ans =
           2.0000
          -1.0000
           1.0000

$\Box$

Eksempel

MATLAB kan dog give overraskende løsninger. I tilfældet, hvor A = [9 8 7, 6 5 4; 3 2 1] er determinanten af A nul. Tidligere blev b sat lig med A*z', hvor z = [ -1 0 1]. For at efterprøve dette skrives:

     w = A\b

Istedet for at give en advarsel omkring A's singularitet, beregnes følgende svar, som ikke svarer til det z' man måske forventer:

     w =
         0.4998
        -2.9996
         2.4998

I dette tilfælde er løsningsrummet én-dimensionalt, så der findes uendelig mange løsninger. MATLAB finder blot en af disse. Havde man istedet spurgt efter b'/A ville man derimod få advarslen:

   Warning: Matrix is singular to working precision.

$\Box$

Anvendelse af potens

Symbolet $\hat{ }$ anvendes til at angive potenser. MATLAB tillader udtryk af typen A $\hat{ }$ p, hvor A er en matrix og p en skalar. Dog er der også indbygget muligheder for tilsvarende udtryk, hvor A er en skalar og p en matrix. Hvor både A og p er matricer kan operationen ikke finde sted og der gives en fejlmeddelelse.

Eksempel

Matricen A = [9 8 7;6 5 4;3 2 1] opløftes til 2. potens og benævnes B.

     B = A^2

som giver

     B =
         150    126     102
         96     81      66
         42     36      30

$\Box$