Tabeloperationer

Tabeloperationer dækker en række yderligere operationer, hvor der opereres enkeltvis på elementerne. En matrix eller vektor, hvorpå der opereres elementvis kaldes her for en tabel. For regneoperationerne addition og subtraktion er der ingen ændring i syntaksen, men for de resterende operationer tilføjes et punktum til operationssymbolet for at indikere, at der er tale om en tabeloperation og ikke en matrixoperation.

Multiplikation og division

Symbolet .* anvendes til elementvis multiplikation. Det er stadigvæk en forudsætning at tabellerne, der indgår som faktorer har ens dimension. Dette skal forståes på den måde at de to faktorer f.eks. begge skal være 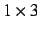$1 \times 3$ vektorer for at operationen lykkes. Igen findes der to udgaver af division. Hvor X og Y er to tabeller findes X./Y og X.\Y

Eksempel

Fra tidligere eksempler kendes y og z, hvor y = [1 2 3] og z = [-1 0 1]. Multiplikation af element for element er givet ved:

     w = y.*z

og der præsenteres svaret:

     w =
         -1    0    3

$\Box$

Eksempel

Tilsvarende gælder for division. Med de y og z variable, der er givet tidligere vil kun den ene divisionoperation give mening:

     v = y.\z

Hvilket resulterer i:

     v =
         -1.0000       0       0.3333

$\Box$

Anvendelse af potenser for tabeller

Elementvis potensbehandling angives ved .$\hat{ }$

Eksempel

Her kommer en række kombinationer, hvor der kan anvendes potenser. Variablen y givet ved y =[1 2 3] som i forrige eksempel og variablen x = [3 1 2] tilføjes.

    w  = y.^x

Herved fås svaret

     w  = 
          1   2   9

Der kan ligeledes indgå en skalar:

     w  = y.^3

som giver svaret

     w  = 
          1   8   27

Endelig den omvendte anvendelse af skalar

     w  = 3.^x

Hvilket resulterer i svaret

     w  = 
          27   3   9

$\Box$

Relationsoperationer

For skalarer og matricer giver MATLAB mulighed for 6 relationsoperationer. Disse operationer giver mening under forudsætning, at matricerne er af samme dimension. En skalar kan dog sammenlignes med en matrix, da vil skalaren blot blive sammenlignet med hvert element i matricen. Bemærk at et enkelt stående lighedstegn allerede anvendes som en tildelingsoperator (f.eks. i forrige eksempel tildeles variablen w bl.a. resultatet af operationen y.$\hat{ }$ 3), derfor benyttes det dobbelte lighedstegn som sammenligning operatoren. MATLAB sammenligner matricerne elementvis og resultatet er en matrix, hvis elementer udgøres af 0'er og 1'er, hvor 0 repræsentere 'falsk' og 1 'sandt'.

$<$

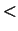
mindre end

$<=$

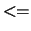
mindre end eller lig med

$>$

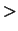
større end

$>=$

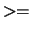
større end eller lig med

$==$

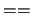
lig med

$\sim =$

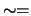
forskellig fra

Eksempel

Lad tabellen y være defineret ved y = [5 2 1] og da pi (den indbygget standardfunktion for 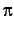$\pi$) er en skalar, kan hvert element i y sammenlignes med denne. En kommando af form:

     y <= pi

vil resultere i svaret:

     ans =
           0    1    1

$\Box$

Matematiske funktioner

MATLAB inkluderer en del matematiske funktioner, heriblandt diverse trigonometriske funktioner. Hvor funktionen anvendes på tabeller, sker dette elementvis.

• Trigonometriske funktioner. Her præsenteres et udvalg
  • sin står for sinusfunktionen. Tilsvarende for cos og tan.

  • asin er arcsinus. Ligeledes gives der acos og atan.

  • sinh står for funktionen sinus hyberbolsk. Igen findes der varianterne cosh og tanh

• Udvalg af elementære funktioner
  • abs Den absolutte værdi.

  • sqrt Kvadratrod.

  • exp Eksponential funktionen med base e.

  • log Den naturlige logoritme.

  • log10 Logoritme med base 10.

Eksempel

Variablen z er stadigvæk defineret som z = [-1 0 1]. Ved anvendelse af en trigonometrisk funktion på z vil elementerne blive behandlet enkeltvis. Kommandoen

     sin(z)

vil resultere i

     ans  =
            -0.8415    0    0.8415

$\Box$

Eksempel

Ganske tilsvarende vil det gøre sig gældende for de elementære funktioner. Her bliver vektoren z givet i eksemplet ovenfor, igen anvendt.

     sqrt(z)

giver

     ans =
           0 + 1.0000i     0    1.0000

Bemærk, at MATLAB, ikke giver en fejlmeddelelse for at skulle tage kvadratroden af et negativt tal. I stedet indenføres komplekse tal i løsningen. Dette må brugeren selv være opmærksom på, hvis de komplekse løsninger ikke ønskes.

$\Box$