Ikke-lineær ligninger og optimeringsfunktioner

I standardpakken af MATLAB gives der 3 hjælpefunktioner for ikke-lineære funktioner. Disse er som følger:

• fminbnd('fname',x1,x2) Denne funktion beregner minimum for funktionen angivet i en M-fil. Funktionen må kun være afhængig af en variabel. Intervalet, hvori minimum ønskes fundet, angives ved grænserne x1 og x2.

• fminsearch('fname',x0) fminsearch finder minimum for funktioner af flere variable. Der angives et begyndelsesgæt x0, hvori metoden tager udgangspunkt. fminsearch anvender en simplex-søgemetode udarbejdet af Nelder og Mead.

• fzero('fname',x0) Der findes et nulpunkt for funktioner af en varibel, nær ved begyndelsesgættet x0.

Eksempel

En M-fil ved navn trifil.m er oprettet for at repræsentere funktionen:

$$f(x) = - \sin^3(x)\cos(x)$$

På figur 4.1 ses en skitse af denne funktion.

Figure: Funktionen $f(x) = - \sin^3(x)\cos(x)$

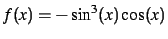
Først ønskes det at finde minimum i intervalet $[0, \frac{\pi}{2}]$. Der skrives:

      m = fminbnd('trifil', 0, pi/2)

og der gives svaret

      m =
            1.0472

Bemærk at dette kun er et lokalt minimum. Herefter søges der efter et nulpunkt udfra et begyndelsesgæt på værdien $\frac{\pi}{8}$.

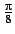      n = fzero('trifil', pi/8)

Det svar der beregnes er :

      n = 
          1.5884e-16

Dette er ikke det præcise nulpunkt (som er i nul), men nulpunktet forekommer i en vendetangent og nulpunktsalgoritmen har derfor svært ved finde nulpunktet. Se figur 4.1. Bemærk, at MATLAB kun finder et nulpunkt ad gangen. Det er brugeren, der selv må overskue om der kunne være flere og hvor det er hensigtsmæssigt at gætte på en løsning. I dette eksempel kan der således bl.a. findes endnu et nulpunkt ved:

      p = fzero('trifil', 2)

der giver svaret:

      p = 
          1.5708

$\Box$