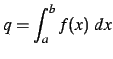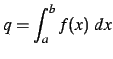



Next: Ikke-lineær ligninger og optimeringsfunktioner
Up: Hjælpefunktioner til matematiske funktioner
Previous: Hjælpefunktioner til matematiske funktioner
Contents
Index
Numerisk integration
Der findes to metoder til numerisk integration af en funktion
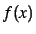 over et givet interval. Denne beregning kaldes for kvadratur. Der
løses problemer, der matematisk formuleres som
De to metoder er:
over et givet interval. Denne beregning kaldes for kvadratur. Der
løses problemer, der matematisk formuleres som
De to metoder er:
- quad('fname',a,b) - Funktionen finder en Simpson
approksimation som løsningen. Filnavnet i kursiv skal erstattes
med navnet på den M-fil, der repræsenterer funktionen
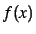 . De
enkelte citationstegn er vigtige og fortæller MATLAB, at dette er
navnet på en M-fil og ikke en indbygget funktion i MATLAB. Intervalet
er angivet her fra a til b.
. De
enkelte citationstegn er vigtige og fortæller MATLAB, at dette er
navnet på en M-fil og ikke en indbygget funktion i MATLAB. Intervalet
er angivet her fra a til b.
- quad8('fname',a,b) - Her benyttes en rekursiv
Newton-Cotes metode til løsningen. Der gælder de samme forhold for quad8 som for quad omkring funktionsfilen og intervalangivelser.
Antallet af rekursioner for begge hjælpfunktioner er begrænset og det kan
ske, at dette antal ikke
er nok til at en løsning kan findes. MATLAB vil da give en fejlmeddelelse.
Det er muligt at ændre loftet for det maksimale antal iterationer en
numerisk løsningsmetode skal gennemløbe. Ændringen skal ske som en ændring
af en specifik vektor, der er defineret af MATLAB. Se MATLABs egne manualer
vedrørende optionsvektor.
Arealet under en positiv funktion defineret med funktionsfilen funkfil.m i
intervalet ![$ [0,1]$](img19.gif) ønskes bestemt. På kommandolinien skrives nu:
ønskes bestemt. På kommandolinien skrives nu:
quad('funkfil',0,1)
Hvorefter at MATLAB beregner resultatet til :
ans =
3.1416
Den anden metode vil ved kommandoen quad8('funkfil',0,1)i dette
tilfælde producere tilsvarende:
ans =
3.1416





Next: Ikke-lineær ligninger og optimeringsfunktioner
Up: Hjælpefunktioner til matematiske funktioner
Previous: Hjælpefunktioner til matematiske funktioner
Contents
Index
Bo Jakobsen
2000-08-15