
A glass is a solid that is disordered on the atomic scale. In fact its structure is not very different from a liquid as can be seen in the figure below. A glass is formed when a liquid is cooled in such a way as to avoid crystallization; generally, this means, rapid cooling. Rapid cooling is necessary because the crystal state is the thermodynamically favoured state below the melting point. But to form a crystal there first must be nucleation of nanosized crystals followed by growth of these. The nucleation takes time, even below the melting point. The further below the melting point, the greater the driving force, but also the slower the dynamics of the liquid (which is now termed 'supercooled'). There is a temperature window where crystallization is most favoured. Once the liquid is cooled below that, crystallization is less likely. Instead the viscosity of the supercooled liquid (SCL) increases dramatically (in an almost divergent fashion) until the material is effectively solid. By convention this "glass transition" temperature is defined as the temperature where the viscosity is 10^13 Poise. The nature of the glass transition is far from being understood although simulations and models have recently provided much insight.
It was only in 1960 that it became possible to make metallic glasses. Because metals are simpler than, for example covalent-network glasses like silica (their liquid and crystal phases can largely be describe in terms of the packing of spheres), it is much easier for crystallization to occur in them. Thus the first MGs had to be cooled around 10^6K/s using special techniques which only allowed thin strips to be created. In the early 1990's families of alloys were discovered (containing three or more elements) which could form glasses at much more modest cooling rates, 10-100K/s. Now larger "bulk" samples could be created, thus, Bulk Metallic Glasses.
| Example of a configuration of Mg-Cu metallic glass created by simulated cooling from the melt. There is 15% Cu out of 2048 atoms. Notice that there is no obvious order to the atoms. In fact there is a certain amount of short-range order, but not the long-range order that charaterizes crystals. |  |
There are two issues to consider. The first is how to model the interactions between atoms. Ideally one would use a quantum-mechanical treatment, for example density function theory, to be sure of good accuracy, but we want to be able to simulation large systems. So we use a semi-empirical potential called effective medium theory (EMT) as implemented in the ASAP code. This code was already in existence but did not have parameters for Mg. Moreover the Cu parameters were optimized for the study of crystalline processes in Cu whereas these have no relevance in the amorphous case, so we refitted Cu and fitted Mg to reproduce lattice constants and cohesive energies of the pure elements and two intermetallic alloys, as well as elastic constants of the pure elements. The data to be matched came from experiment and DFT calculations.
The second issue is, once you have an interatomic potential that you trust, how do you create glassy configurations that you trust? Ideally we would simulate the actual cooling process, at the actual cooling rate. In fact, we do simulate the cooling but because of the usual time-scale problem in molecular dynamics we must cool several orders of magnitude faster. The question is then, how much of a problem this is.
| The figure to the right shows the specific heat from a cooling run. It exhibits the drop associated with the glass transition and in fact this happens at about the right temperature, although the transition is very wide. Slower cooling reduces this width, but the real issue is the potential energy of the resulting zero-temperature amorphous state. |  |
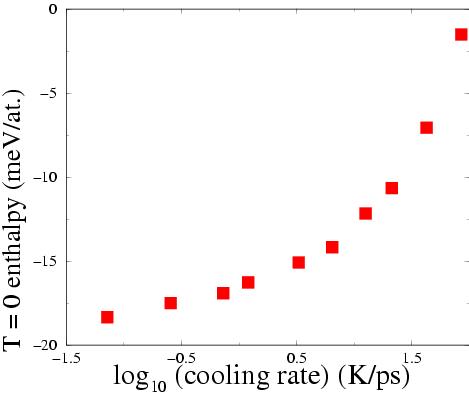
| This figure shows the final potential energy as a function of cooling rate. We have generally been happy enough to use the second or third slowest rate, but have observed effects of metastability (aging effects) in some simulations, namely ones at slow strain rates and high temperatures, where there is time for further annealing to take place. Hence we have created some samples at the slowest cooling rates, corresponding to 0.04K/ps. The difference this makes in the potential energy is about 2 meV per atom, which does not seem large, but this corresponds to the excess energy induced by deformation in the slow/high-temperature simulations alluded to above (the excess energy is generally higher than this under other conditions). |
 |
| Our largest glass sample, with a little over one million atoms. This has only been created at the higher cooling rate of 0.75k/ps. |  |
| Even before we get to shear-banding, there is much to be understood about plastic deformation at a fundamental level. And before examing plastic deformation, it is wise to first study elastic deformation. This figure shows the bulk modulus and shear modulus for a range of systems covering the entire composition range of the binary system. The open (filled) symbols show values for unrelaxed(relaxed) elastic constants. It can be seen that the ability for the atoms to move around under strain reduces the shear modulus by about a factor of two. It can also be seen that this does not occur in the pure elements where crystallization occurred. |  | |
| This figure shows the temperature dependence of the bulk and shear moduli for 15% Cu metallic glass, obtained by simulation. The shear modulus vanishes as the glass transition temperature is approached, while the bulk modulus does not vanish but does have a noticeable feature in the temperature dependence at Tg (the arrow). |  |
| After a couple of percent strain, deviations from linear elasticity can be seen in the stress-strain curves. Examples of stress-strain curves are shown on the right, for different system-sizes, all at zero temperature. While at the largest systems we see a relatively smooth stress-strain curve, for small systems we see the signatures of individual events: sharp drops in stress as each one occurs. | 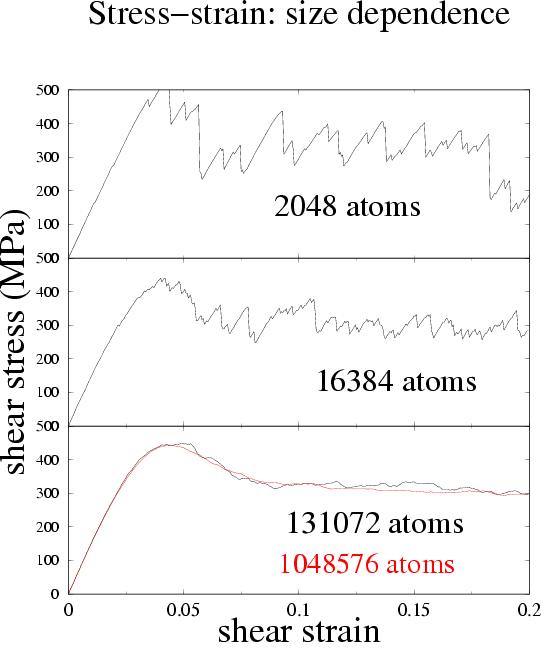 |
| Using a technique to measure reaction pathways we can computer the energy along the path from initial to final state. A typical energy profile looks like this. The lower left inset shows the atoms that took part in this event. The method we use is a constant-stress method (so I should really say enthalpy instead of energy because there's a PV-type term added on to account for the stress); strss is therefore a parameter in the calculations and the results are a funcion of stress. In particular the barrier height for the transition is a function of stress, which is plotted in the upper-right inset. This decreases and vanishes at a critical stress. |  |
Another quantitiy we measure for each event is the amount of plastic strain associated with it. This can be expressed as a volume, which we call the slip volume, by multiplying by the system size (this is reasonable because for a localized event the plastic strain felt at the boundaries is inversely proportional to the volume of the system). Below on the left are histograms showing the distributions of critical stress and slip volume. The heavier lines represent eents from the "steady-state" part of the stress-strain curve, after the intial hump. The figure below and to the right shows again the distribution of critical stresses (measured from studying many events in a small system) along with the distribution of actual stress within a large system (but averaged over sub-volumes corresponding to the small system). The distributions are very similar (in particular their means are the same). Note that the internal stress distribution is narrower at the start of deformation (and of course its mean is zero). The picture this suggests to us is that in the course of deformation the internal stress distribution of the sample evolves to match the distribution of critical stresses.
 |
 |
Apart from the work studying individual events just mentioned, there have being ongoing simulations at finite temperature, with various temperatures and strain rates, whose purpose is to obtain a constitutive law for plastic deformation in BMGs. These simulations involve periodic boundary conditions and are basically simulating homogeneous deformation (in the usual sense of homogeneous deformation when applied to metallic glasses; it is homogeneous at scales larger than the individual events). In addition, we have been trying to simulation inhomogeneous deformation, in particular, we have been trying to observe shear banding. The simulations aim to mimic onventional tensile testing, on the nano-scale, so free surfaces are used.
It turned out a little difficult. Taking an initial cube containing 131000 atoms, one has to nearly double the length in the strain direction before any kind of localization of strain occurs. And when it does occur, it tends to be the standard necking instability. This continues until the sample breaks completely as can be seen in this movie (this particular sample had a notch which was intended to help nucleate a shear band more easily).
To identify shear banding it is useful to display only the atoms actively part in plastic deformation at any time. This movie does so. There is some evidence of shear bands at 45 degree angles and starting from the notch at least in the middle stage of the deformation. Towards the end all of the deformation is in the necked region, which is certainly a form of localization, but not shear banding.
We have, however, found clearer evidence of shear banding in samples which are very thin, so that they are almost two-dimensional. An example movie is movie. Here there were periodic boundary conditions in the out-of-plane direction, so the conditions are plane-strain. Another example had free surfaces in this direction, making it a plane-stress deofmration. Here there was even more dramatic shear-banding. Note that the sample does neck eventaully, but the necking region is not included in the slightly zoomed-in view of this movie.
We are continuing to run simulations to investigate under what conditions shear bands form. There are also some artifacts of high strain rates which we would like to remove by running at slower rates. There are also many things to determine about the shear bands, for example whether there is localized heating or not.
This page was last modified on 6/12/04